(알고리즘) 위상 정렬 Topological Sort + C++ 예제

위상 정렬(Topological Sort)이란?

여태까지 정렬 기준이 였다면 **위상정렬의 정렬 기준은 ‘위상’**이다. 여기서 위상이란 incoming edge의 수를 의미한다.

위상 정렬은 Directed Acyclic Graph(DAG)에서만 가능한 정렬방법이다.
DAG란 각 edge가 방향을 가지고 있는데 cycle이 발생하지 않는 경우를 말한다.
Cycle이 있으면 무한 루프를 발생시킬 것이다!!
보통 일의 순서를 정하는 알고리즘에서 많이 사용된다.

Topological Sorting 알고리즘

알고리즘의 과정은 다음과 같다.

각 vertex의 위상(incoming edge의 수)를 저장한다.
정점(위상이 0인 노드)을 다 큐에 넣어준다.
큐에서 노드를 하나씩 꺼내서 위상정렬에 넣어준다.
꺼낸 노드와 연결된 노드의 위상을 하나씩 낮춰주고 엣지를 없애준다.
위상이 0인 노드를 큐에 다시 넣어준다.
3번부터 5번을 큐가 빌 때까지 반복한다.

예시

다음과 같은 그래프에 대해 위상 정렬을 진행해보자.

위상 0인 친구 큐에 넣기

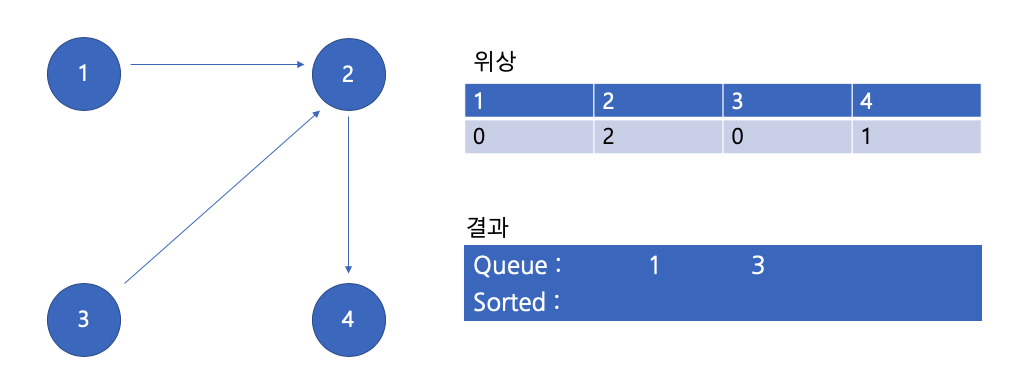
큐에서 1 꺼내기

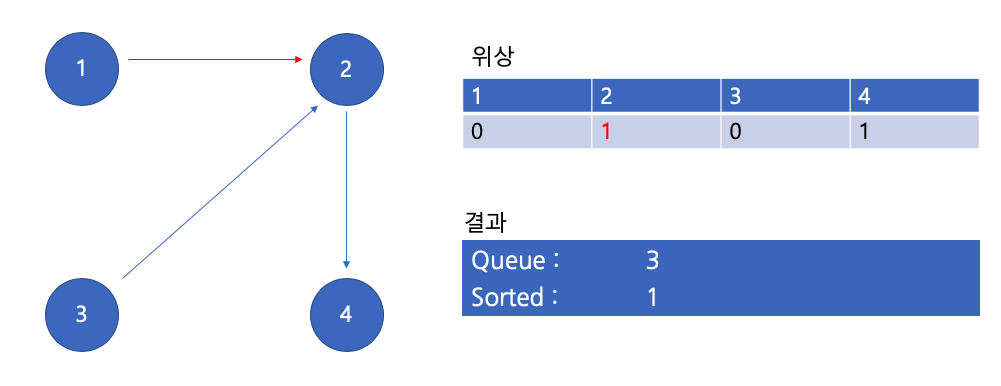
이 때는 위상이 0인 친구가 없으므로 큐에 아무 값도 들어가지 않는다.

큐에서 3 꺼내기

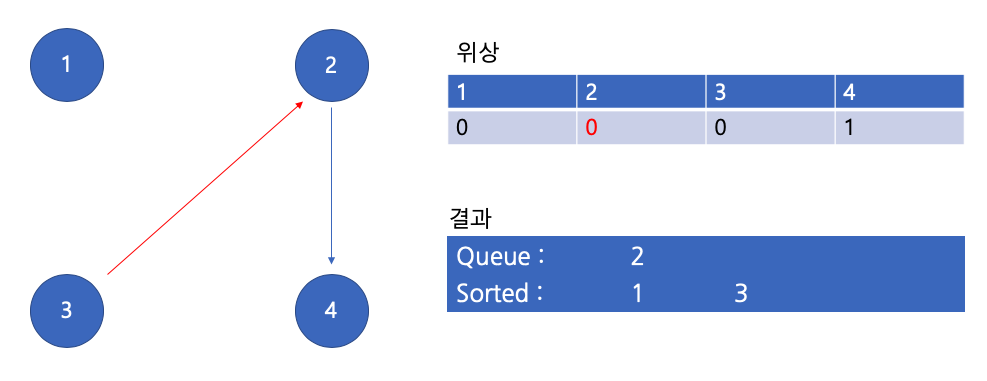
큐에서 2 꺼내기

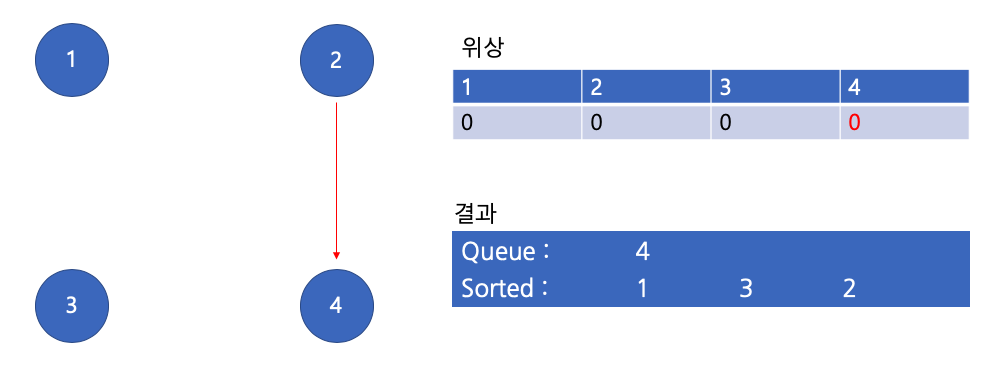
이제 큐에 아무것도 없으므로 최종 위상 정렬된 결과(1,3,2,4)를 얻을 수 있다.

위상정렬 관련 문제 (백준 2252번 줄세우기)

백준 2252번 줄세우기 링크

링크드 리스트 사용

#include <cstdio>
#include <queue>

using namespace std;

int* in;
queue<int> q;


struct Node {
    int data;
    Node* next, * prev;
    Node() {
        next = prev = NULL;
        data = 0;
    }
    Node(int i, Node* ptr){
        data = i;
        prev = ptr;
        next = ptr->next;
        next->prev = prev->next = this;
    }
};

struct LinkedList {
    Node *head;
    Node *tail;
    LinkedList() {
        head = new Node();
        tail = new Node();
        head->next = tail;
        tail->prev = head;
    }
    void insert(int i) {
        new Node(i, tail->prev);
    }
};


int main(){
    int N, M, v1, v2;
    scanf("%d %d", &N, &M);
    LinkedList **list = new LinkedList*[N+1];
    for(int i = 0; i < N + 1; i++)list[i] = new LinkedList();
    in = new int[N+1];
    for(int i = 0; i < N + 1; i++)in[i] = 0;
    for(int i = 0 ; i < M; i++){
        scanf("%d %d", &v1, &v2);
        list[v1]->insert(v2);
        in[v2] ++;
    }
    for(int i = 1; i <N+1; i++){
        if(in[i] == 0) q.push(i);
    }

    while(!q.empty()){
        int temp = q.front();
        printf("%d ", temp);
        q.pop();
        Node* tmp = list[temp]->head;
        while (tmp->next != NULL) {
            in[tmp->data] --;
            if(in[tmp->data] == 0) q.push(tmp->data);
            tmp = tmp->next;
        }
    }
}

이중 벡터를 이용한 코드

#include <cstdio>
#include <queue>
#include <vector>

using namespace std;

int* in;
queue<int> q;

int main(){
    int N, M, v1, v2;
    scanf("%d %d", &N, &M);
    vector<vector<int> > v;
    for(int i = 0; i < N + 1; i++)v.push_back(vector<int>());
    in = new int[N+1];
    for(int i = 0; i < N + 1; i++)in[i] = 0;
    for(int i = 0 ; i < M; i++){
        scanf("%d %d", &v1, &v2);
        v[v1].push_back(v2);
        in[v2] ++;
    }
    for(int i = 1; i <N+1; i++){
        if(in[i] == 0) q.push(i);
    }

    while(!q.empty()){
        int temp = q.front();
        printf("%d ", temp);
        q.pop();
        for(int i = 0; i < v[temp].size(); i++){
            if(--in[v[temp][i]] == 0)q.push(v[temp][i]);
        }
    }
}

결과

이중 벡터 써도 각 벡터마다 사이즈를 달리할 수 있다. 그렇다면 확실히 따로 링크드 리스트 쓰는 것보다 그냥 벡터를 쓰는 게 좋다!!

느낀점

정리하기 전까지 왜 위상정렬이 일의 순위를 정해주는 줄 몰랐다.
위상정렬은 의존성이 없는 일부터 시작해서 의존성이 낮은 애들부터 하나씩 처리해가는 알고리즘이다.
나중에 분명히 쓰일 일이 있을텐데 공부할 수 있게 되서 좋았다 ㅎㅎ
위상정렬 모르면 못풀 문제들이 있을거 같다. 이제는 무서워 하지 말고 달려보자 ㅎㅎ