💪
(알고리즘) Union Find 알고리즘 강화버전 - Rank, Path Compression 사용
May 19, 2019
기존 Rank 활용 방법
- 이전 포스트에서 그림으로 표현했듯이, union과 find를 계속 진행하다보면 worst case에서는 그림과 같이 나오게 된다.
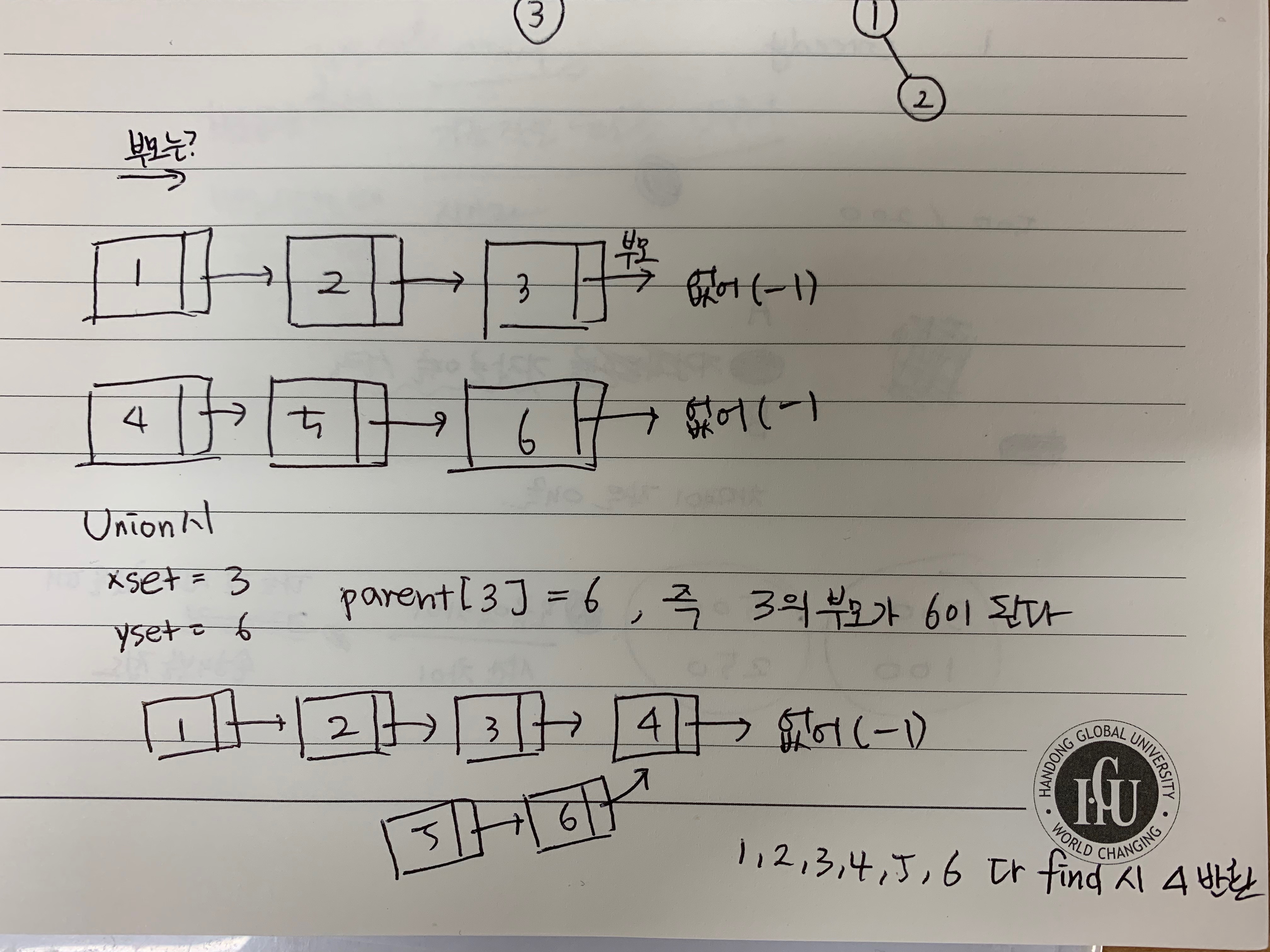
- 그림과 같이 작은 트리가 큰 트리에 붙는 형식으로 이는 Linked List의 형태를 띄게 된다.
- 이것의 시간 복잡도는 O(log n) 만큼 걸리게 된다.
- 이를 union by rank라고 한다.
Path Compression 활용 방법
- 다른 방법이 또 있다면 path compression이다.
- 이 방법은 find()가 호출될 때 tree를 납짝하게 만드는 것이다.
- find()가 x에 대해서 호출되면 x로부터 root node를 찾기 시작한다.
- 찾아서 root node를 반환시켜준다.
- 그리고 root node에 이어붙이기 때문에 Rank 활용 때처럼 중간에 있는 친구들을 다 search하지 않아도 된다는 장점이 있다.
Rank와 Path Compression을 활용하면 기존의 방법보다 훨씬 효율적인 코드를 짤 수 있다!
Rank와 Path Compression 활용 코드
이 코드는 기존 코드에 parent와 rank의 정보를 담고 있는 subset이 추가되었다.
//각 Edge의 정보가 담긴 struct이다.
struct Edge{
int src, dest;
};
//각 Graph의 정보가 담긴 struct이다.
struct Graph{
int V, E;
struct Edge* edge;
};
//parent와 rank 정보가 담긴 struct이다.
struct subset {
int parent;
int rank;
};
//Graph를 생성해서 반환해주는 역할을 하는 함수이다.
//V는 vertex 개수, E는 edge의 개수를 의미한다.
struct Graph* createGraph(int V, int E){
//그래프 공간 할당!
struct Graph* graph = (struct Graph*) malloc( sizeof ( struct Graph));
//그래프의 크기를 주어진 정보를 이용해 정해준다.
graph->V = V;
graph->E = E;
//그래프의 edge 개수만큼 Edge의 공간을 할당해준다.
graph->edge = (struct Edge*) malloc ( graph -> E * (struct Edge));
//만든 그래프를 반환해준다.
return graph;
}
//Path compression의 장점을 활용해 root node를 찾아주는 역할을 하는 친구다.
int find(struct subset subsets[], int i){
//root node가 아니면 root node 찾을 때까지 recursive하세요.
if(subsets[i].parent != i)subsets[i].parent = find(subsets,subsets[i].parent);
//root node를 반환해주세요.
return subsets[i].parent;
}
//이번에는 rank를 이용해서 합쳐준다.
void Union(struct subset subsets[], int x, int y){
//각각 root node를 찾아줍니다.
int xroot = find(subsets, x);
int yroot = find(subsets, y);
//root node의 rank에 따라 누가 밑으로 붙을지 정합니다.
if(subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot;
else if(subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot;
//두개가 같으면 x를 위로 올려주고 x의 root node rank를 하나 더해줍니다.
else{
subsets[yroot].parent = xroot;
subsets[xroot].rank ++;
}
}
//Cycle을 확인해주는 함수
int isCycle(struct Graph* graph){
int V = graph->V;
int E = graph->E;
//subset의 크기를 정해줍니다.
struct subset *subsets = (struct subset*) malloc( V * sizeof(struct subset) );
//초기 rank를 0으로 또 parent를 자기 자신으로 즉 자기를 rootnode로 설정한다.
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
//그래프의 Edge를 쭉 훑어봅시다.
for(int e = 0; i < E; ++i)
{
//Edge의 src와 dest node가 같은 graph에 속해있나 봅시다.
int x = find(subsets, graph->edge[e].src);
int y = find(subsets, graph->edge[e].dest);
//같으면 Cycle이 있는겁니다.
if (x == y) return 1;
//아니면 두 그래프를 합쳐요!
Union(subsets, x, y);
}
return 0;
}
int main(){
int V = 3, E = 3;
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// add edge 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if(isCycle(graph)) printf("사이클 있어요~");
else printf("사이클 없어요~");
}위 과정을 통하면 log n 이 중간에 있는 노드를 더 적게 가므로 더 짧은 log n이 된다! 쉽지 않다…ㅎㅎ
느낀점
- 진짜 조금 더 빠르게 할려는 방법을 찾는게 대박이다…
- 이제 본격적으로 이거를 그래프 알고리즘에 써먹어봐야겠다.